DERIVATIVES OF
TRIGONOMETRIC FUNCTIONS
The derivative of sin x
| d dx |
sin x | = cos x |
To prove that, we will apply the definition of the derivative (Lesson 5). First, we will calculate the difference quotient.
| sin (x + h) − sin x h |
= |  |
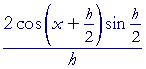, Problem 1, |
| = |  |
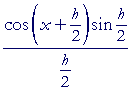, on dividing numerator and denominator by 2, |
|
| = |  |
||
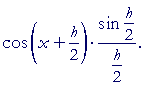We will now take the limit as h 
0. But the limit of a product is equal to the product of the limits. (Lesson 2.) And the factor on the right has the form sin θ/θ. Therefore, according to the Lemma, as h 0 its limit is 1. Therefore,
0. But the limit of a product is equal to the product of the limits. (Lesson 2.) And the factor on the right has the form sin θ/θ. Therefore, according to the Lemma, as h 0 its limit is 1. Therefore,| d dx |
sin x | = cos x. | what about knowing more ?? from here http://www.themathpage.com/acalc/sine.htm#sine |
No comments:
Post a Comment